Page 113 - 6285

P(,)
1,00
d 1 = 2,8

1

 1 =  2 = 1

d 2 = 0,3
2
0,5

–5 –4 –3 –2 –1 0 1 2 3 4 5
, логіти
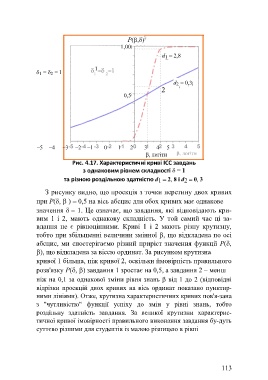
Рис. 4.17. Характеристичні криві ICC завдань
з однаковим рівнем складності  = 1
та різною роздільною здатністю d 1  2, 8 і d 2  0, 3

З рисунку видно, що проекція з точки перетину двох кривих
при P(,  )  0,5 на вісь абсцис для обох кривих має однакове

значення  1. Це означає, що завдання, які відповідають кри-
вим 1 і 2, мають однакову складність. У той самий час ці за-
вдання не є рівноцінними. Криві 1 і 2 мають різну крутизну,
тобто при збільшенні величини змінної , що відкладена по осі
абсцис, ми спостерігаємо різний приріст значення функції P(,
), що відкладена за віссю ординат. За рисунком крутизна

кривої 1 більша, ніж кривої 2, оскільки ймовірність правильного
розв'язку P(, ) завдання 1 зростає на 0,5, а завдання 2 – менш

ніж на 0,1 за однакової зміни рівня знань  від 1 до 2 (відповідні
відрізки проекцій двох кривих на вісь ординат показано пунктир-
ними лініями). Отже, крутизна характеристичних кривих пов'я-зана
з "чутливістю" функції успіху до змін у рівні знань, тобто
роздільну здатність завдання. За великої крутизни характерис-
тичної кривої імовірності правильного виконання завдання бу-дуть
суттєво різними для студентів із малою різницею в рівні

113