Page 109 - 6285

Для характеристики рівня знань студента й складності зав-
дання до теорії введено нові змінні  і , пов'язані з S і t співвід-
ношеннями:

 ln S ,  ln t. (4.10)

Введення змінних  і  у такому вигляді дає можливість харак-
теризувати рівень знань і складність завдання однаковими без-
розмірними одиницями, які дістали назву логітів [45]. Це дозво-
ляє відображати розподіли знань студентів і складності завдань
в одній шкалі та досліджувати одночасний вплив цих параметрів
на функцію успіху P(, ). Підставивши (3.10) у вигляді

S  exp() і t  exp() до (3.9), отримаємо:
1
.
P(,  )  1 exp() (4.11)

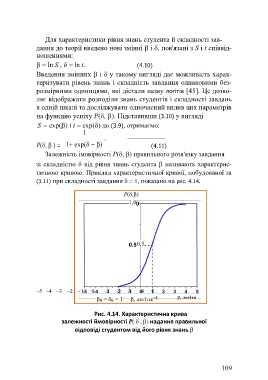
Залежність імовірності P(, ) правильного розв'язку завдання

зі складністю  від рівня знань студента  називають характерис-
тичною кривою. Приклад характеристичної кривої, побудованої за
(3.11) при складності завдання  1, показано на рис. 4.14.

P(,)

1,0

0,5

–5 –4 –3 –2 –1 0 1 2 3 4 5
 0 =  0 = 1 , логіти

Рис. 4.14. Характеристична крива
залежності ймовірності P(  , ) надання правильної
відповіді студентом від його рівня знань 

109