Page 115 - 6285

1,0

P(,) d = 2 d = 0,5

0,5

d = 1

–3 –2 –1 0 1 2 3
, логіти

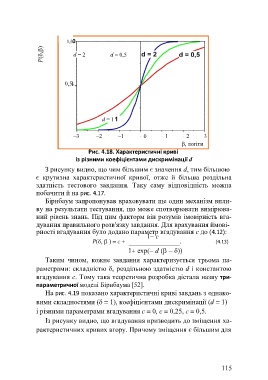
Рис. 4.18. Характеристичні криві
із різними коефіцієнтами дискримінації d

З рисунку видно, що чим більшим є значення d, тим більшою
є крутизна характеристичної кривої, отже й більша роздільна
здатність тестового завдання. Таку саму відповідність можна
побачити й на рис. 4.17.

Бірнбаум запропонував враховувати ще один механізм впли-
ву на результати тестування, що може спотворювати вимірюва-
ний рівень знань. Під цим факторм він розумів імовірність вга-
дування правильного розв'язку завдання. Для врахування ймові-
рності вгадування було додано параметр вгадування с до (4.12):
1 c
P(,  )  c  . (4.13)

1 exp( d ())

Таким чином, кожне завдання характеризується трьома па-
раметрами: складністю , роздільною здатністю d і константою
вгадування с. Тому така теоретична розробка дістала назву три-
параметричної моделі Бірнбаума [52].

На рис. 4.19 показано характеристичні криві завдань з однако-
вими складностями ( 1), коефіцієнтами дискримінації (d  1)

і різними параметрами вгадування c  0, c  0,25, c  0,5.

Із рисунку видно, що вгадування призводить до зміщення ха-
рактеристичних кривих вгору. Причому зміщення є більшим для

115