Page 162 - 6197

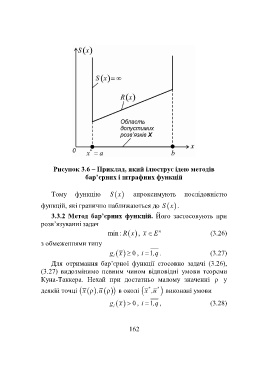
Рисунок 3.6 – Приклад, який ілюструє ідею методів
бар’єрних і штрафних функцій

Тому функцію S   x апроксимують послідовністю
S
функцій, які гранично наближаються до   x .
3.3.2 Метод бар’єрних функцій. Його застосовують при
розв’язуванні задач
n
min : R   x , x  E (3.26)
з обмеженнями типу
g   0x  , i  1,q . (3.27)
i
Для отримання бар’єрної функції стосовно задачі (3.26),
(3.27) видозмінимо певним чином відповідні умови теореми
Куна-Таккера. Нехай при достатньо малому значенні  у

*
 x 
,u 
деякій точці     в околі  x ,u *  виконані умови
g   0x  , i  1,q , (3.28)
i

162