Page 203 - 5637

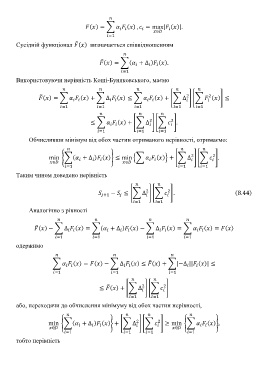
( ) = ( ) , = max| ( )|.

⋳

Сусідній функціонал ( ) визначається співвідношенням

( ) = ( + ∆ ) ( ).

Використовуючи нерівність Коші-Буняковського, маємо

( ) = ( ) + ∆ ( ) ≤ ( ) + ∆ ( ) ≤

≤ ( ) + ∆ .

Обчисливши мінімум від обох частин отриманого нерівності, отримаємо:

min ( + ∆ ) ( ) ≤ min ( ) + ∆ .

⋳ ⋳

Таким чином доведено нерівність

− ≤ ∆ . (8.44)

Аналогічно з рівності

( ) − ∆ ( ) = ( + ∆ ) ( ) − ∆ ( ) = ( ) = ( )

одержимо

( ) = ( ) − ∆ ( ) ≤ ( ) + |−∆ || ( )| ≤

≤ ( ) + ∆

або, переходячи до обчислення мінімуму від обох частин нерівності,

min ( + ∆ ) ( ) + ∆ ≥ min ( ) ,

⋳ ⋳

тобто нерівність