Page 156 - 5637

( , , ) = ( − 0,04) + ( − 4) + ( − 400)

при наявності лінійних обмежень < 0, 03, < 3, < 300. Утворити допоміжну

функцію відповідно до алгоритму

( , , ) = ( , , ) + ( , , ).

тут

( , , ) = (0,03 − , ) + (3 − ) + (300 − ) ,

де = , якщо ≥ 0, і = 0, якщо < 0.

Для вирішення завдання безумовної мінімізації функції ( , , ) застосуємо

алгоритм методу прямого пошуку (§7.4) і програму . Для цього достатньо
лише внести відповідні зміни в процедуру-функцію , яка в цьому випадку буде мати
наступний вигляд.
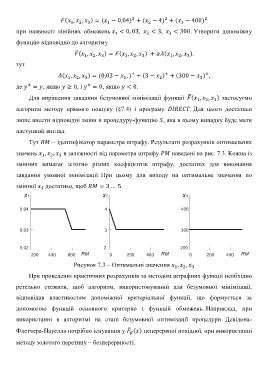
Тут – ідентифікатор параметра штрафу. Результати розрахунків оптимальних
значень , , в залежності від параметра штрафу наведені на рис. 7.3. Кожна із

змінних вимагає істотно різних коефіцієнтів штрафу, достатніх для виконання
завдання умовної мінімізації. При цьому для виходу на оптимальне значення по
змінної достатньо, щоб = 3 … 5.

x1 x2 x3
0,04 4 400
0,03 3 300

0,02 2 200
200 400 600 RM 0 200 400 RM 0 200 400 RM

Рисунок 7.3 – Оптимальні значення , ,

При проведенні практичних розрахунків за методом штрафних функції необхідно
ретельно стежити, щоб алгоритм, використовуваний для безумовної мінімізації,

відповідав властивостям допоміжної критеріальної функції, що формується за

допомогою функцій основного критерію і функцій обмежень. Наприклад, при

використанні в алгоритмі на етапі безумовної оптимізації процедури Девідона-

Флетчера-Пауелла потрібно існування у ( ) неперервної похідної, при використанні

методу золотого перетину – безперервності.