Page 44 - 4974

поверхні циліндра обертання можна прийняти і коло з центром, що
переміщається по осі i . Поверхню циліндра обертання можна вважати і як

обвідну множини сфер однакових радіусів з центрами на осі i .
Циліндр обертання, як і конус обертання, має різні способи утворення і
задання.
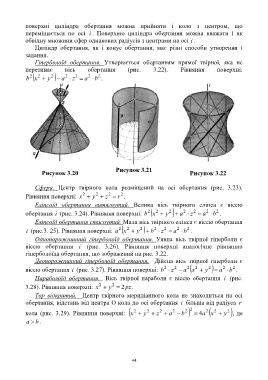
Гіперболоїд обертання. Утворюється обертанням прямої твірної, яка не
перетинає вісь обертання (рис. 3.22). Рівняння поверхні:
2
2
b 2 x  y 2  a  2 z  a 2 b  2 .

Рисунок 3.20 Рисунок 3.21 Рисунок 3.22

Сфера. Центр твірного кола розміщений на осі обертання (рис. 3.23).
2 2 2 2
Рівняння поверхні: x  y  z  r .
Еліпсоїд обертання витягнутий. Велика вісь твірного еліпса є віссю
2 2 2 2 2 2 2
обертання i (рис. 3.24). Рівняння поверхні: xb  y  a  z  a b  .
Еліпсоїд обертання стиснутий. Мала вісь твірного еліпса є віссю обертання
2 2 2 2 2 2 2
i (рис.3. 25). Рівняння поверхні: xa  y  b  z  a b  .
Однопорожнинний гіперболоїд обертання. Уявна вісь твірної гіперболи є
віссю обертання i (рис. 3.26). Рівняння поверхні аналогічне рівнянню
гіперболоїда обертання, що зображений на рис. 3.22.
Двопорожнинний гіперболоїд обертання. Дійсна вісь твірної гіперболи є
2
2
2
2
віссю обертання i (рис. 3.27). Рівняння поверхні: b  z  a 2 x  y 2  a  2 b .
Параболоїд обертання. Вісь твірної параболи є віссю обертання i (рис.
2
2
3.28). Рівняння поверхні: x  y  2 pz.
Тор відкритий. Центр твірного меридіанного кола не знаходиться на осі
обертання, відстань від центра О кола до осі обертання i більша від радіуса r
2
2 2 2 2 2 2 2 2
кола (рис. 3.29). Рівняння поверхні: x  y  z  a  b   4a x  y , де
a  b.

44