Page 26 - 4968

     2
2
k y k  t  ,
4 n 3 n
y  u ,
0 0

 y  k  2k  2k  
n 1 n 1 2 3 4
y k
6
.
Хід роботи
Розв’язати чисельним методом звичайне диференційне
рівняння (методом Рунге-Кута четвертого порядку), побудувати

.
графік  ty на інтервалі t  20;0
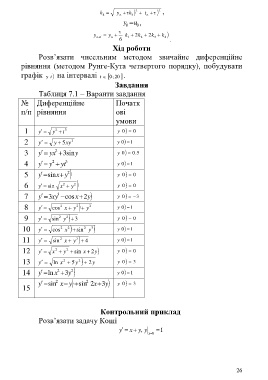
Завдання
Таблиця 7.1 – Варанти завдання
№ Диференційне Початк

п/п рівняння ові
умови


y  2 t  3  0 
1 y y 0

y  y  3   10 
2 5xy y
y   yx   0 
2
3 3 sin y y 5 . 0
y   y  3   10 
2
4 yt y
y   x 2   0 
5 sin y y 0
y    x  2   0 
2
6 sin y y 0
y 3  xy cos x 2  0  
3
7  y y 3

y  2 x  2  y 2   10 
8 cos y y
 2 2  0 
9  y sin   3y y 0
y  2   sin yx  2     10 

3
2
10 cos y
 2 3  4   10 
11  y sin   yx y
y   x  y  x 2  0 
2
2
12 sin  y y 0

y  x  2  2  0 
2
13 ln 5 y y y 3
y    lnx  2    10 
2
14 3y y
y sin  2 x  y sin 2  x 32   y y  0  3
15

Контрольний приклад

Розв’язати задачу Коші

y   x  y , y  1
x 0

26