Page 13 - 4861

tk=100;
%Розв’язання системи диференціальних рівнянь
options=odeset('RelTol',E)
[T,P]=ode45(@Rsol,[0 tk],P0,options,A);
plot(T,P(:,1),T,P(:,2),T,P(:,3),T,P(:,4));
legend('P0','P1','P2','P3')
Лістинг 5.2 – Файл - функція формування матриці А

function F=Rsol(t,x,A)
%Формування матриці правих частин ДР
F=A*x;
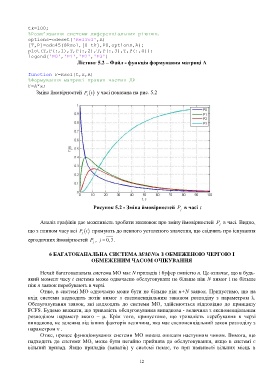
Зміна ймовірностей   t у часі показана на рис. 5.2
P
j

Рисунок 5.2 - Зміна ймовірностей P в часі t
j

Аналіз графіків дає можливість зробити висновок про зміну ймовірностей P в часі. Видно,
j
що з плином часу всі   t прямують до певного усталеного значення, що свідчить про існування
P
j
ергодичних ймовірностей P , j  0, 3.
j

6 БАГАТОКАНАЛЬНА СИСТЕМА M/M/N/n З ОБМЕЖЕНОЮ ЧЕРГОЮ І
ОБМЕЖЕНИМ ЧАСОМ ОЧІКУВАННЯ

Нехай багатоканальна система МО має N приладів і буфер ємністю n. Це означає, що в будь-
який момент часу t система може одночасно обслуговувати не більше ніж N вимог і не більше
ніж n заявок перебувають в черзі.
Отже, в системі МО одночасно може бути не більше ніж n+N заявок. Припустимо, що на
вхід системи надходить потік вимог з експоненціальним законом розподілу з параметром λ.
Обслуговування заявок, які надходять до системи МО, здійснюється відповідно до принципу
FСFS. Будемо вважати, що тривалість обслуговування випадкова - величина з експоненціальним
розподілом параметр якого – μ. Крім того, припустимо, що тривалість перебування в черзі
випадкова, не залежна від інших факторів величина, яка має експоненціальний закон розподілу з
параметром ν .
Отже, процес функціонування системи МО можна описати наступним чином. Вимога, що
надходить до системи МО, може бути негайно прийнята до обслуговування, якщо в системі є
вільний прилад. Якщо приладів (каналів) у системі немає, то при наявності вільних місць в

12