Page 11 - 4861

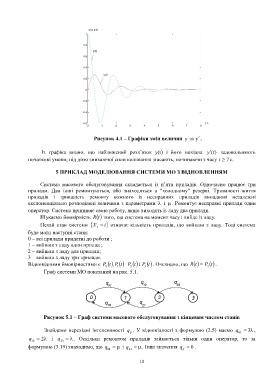
Рисунок 4.1 – Графіки змін величин таy y.

Із графіка видно, що наближений розв’язок y(t) і його похідна y ) (t задовольняють
початкові умови; під дією зникаючої сили коливання згасають, починаючи з часу t 7 с.

5 ПРИКЛАД МОДЕЛЮВАННЯ СИСТЕМИ МО З ВІДНОВЛЕННЯМ

Система масового обслуговування складається із п’яти приладів. Одночасно працює три
прилади. Два інші ремонтуються, або знаходяться в "холодному" резерві. Тривалості життя
приладів і тривалість ремонту кожного із несправних приладів випадкові незалежні
експоненціально розподілені величини з параметрами  і . Ремонтує несправні прилади один
оператор. Система припиняє свою роботу, якщо виходять із ладу два прилади.
Шукаємо ймовірність  tR того, що система на момент часу t вийде із ладу.
 i
Нехай стан системи X  означає кількість приладів, що вийшли з ладу. Тоді система
t
буде мати наступні стани:
0 – всі прилади придатні до роботи ;
1 – вийшов з ладу один прилад ;
2 – вийшли з ладу два прилади;
3 – вийшли з ладу три прилади.
Відповідними ймовірностями є     PtP,tP   Pit  t . Очевидно, що  tR  P  t .
0 1 2 3 3
Граф системи МО показаний на рис. 5.1.

Рисунок 5.1 – Граф системи масового обслуговування з кінцевим числом станів

Знайдемо перехідні інтенсивності q . У відповідності з формулою (2.5) маємо q  3  ,
ij 01
q  2  і q   . Оскільки ремонтом приладів займається тільки один оператор, то за
12 23
формулою (3.19) знаходимо, що q   і q   . Інші значення q  0 .
10 21 ij

10