Page 30 - 4818

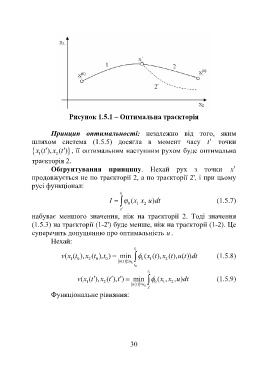
Рисунок 1.5.1 – Оптимальна траєкторія

Принцип оптимальності: незалежно від того, яким
шляхом система (1.5.5) досягла в момент часу t точки
 (), ( )x t 1 x t 2 , її оптимальним наступним рухом буде оптимальна

траєкторія 2.

Обґрунтування принципу. Нехай рух з точки x
продовжується не по траєкторії 2, а по траєкторії 2', і при цьому
русі функціонал:

t 1
0 
I   (xx u )dt (1.5.7)
2
1
t
набуває меншого значення, ніж на траєкторії 2. Тоді значення
(1.5.3) на траєкторії (1-2') буде менше, ніж на траєкторії (1-2). Це
суперечить допущенню про оптимальність u .

Нехай:
t 1
0 
vx x t t  min  ( (), ( ), ())x t x t u t dt (1.5.8)
( ( ), ( ), )t
0
0
2
0
1
ut  1 2
() u
k
t 0
t 1
0 
(( ), ( ), )t
vx x t t   min  ( , , )x x u dt (1.5.9)
1
2
ut  k t 1 2
() u
Функціональне рівняння:

30