Page 68 - 4777

Приклад. Дослідити на найбільше та найменше
2
значення функцію z = ху – y + 3х + 4у у замкненій області D,
межа якої: x = 0, у = 0, x + у = 1.
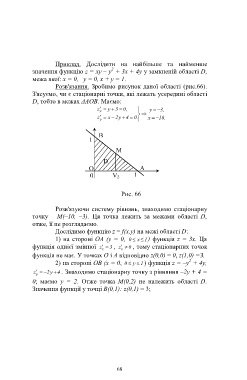
Розв'язання. Зробимо рисунок даної області (рис.66).
З'ясуємо, чи є стаціонарні точки, які лежать усередині області
D, тобто в межах ΔAOB. Маємо:

z  у  3  , 0  у   , 3
х
 

z  х  2 у  4  . 0 х   10 .
у 

B
1
M

D
O A
0 V 2 1

Рис. 66

Розв'язуючи систему рівнянь, знаходимо стаціонарну
точку Μ(–10, –3). Ця точка лежить за межами області D,
отже, її не розглядаємо.
Дослідимо функцію z = f(x,у) на межі області D:
1) на стороні ОА (у = 0, 0  х  1) функція z = 3х. Ця

функція однієї змінної z  , z  , тому стаціонарних точок

0
3
х х
функція не має. У точках О і А відповідно z(0,0) = 0, z(1,0) =З.
2
2) на стороні OВ (x = 0, 0  у  1) функція z = –у + 4у,
z   2 у  4 . Знаходимо стаціонарну точку з рівняння –2у + 4 =

у
0; маємо у = 2. Отже точка Μ(0,2) не належить області D.
Значення функції у точці В(0,1): z(0,1) = 3;

68