Page 111 - 4624

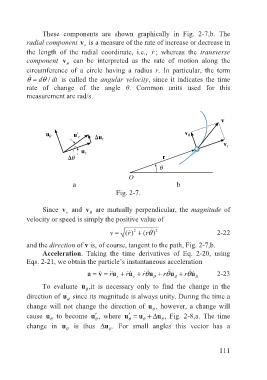
These components are shown graphically in Fig. 2-7,b. The
radial component v is a measure of the rate of increase or decrease in
r
the length of the radial coordinate, i.e., r ɺ; whereas the transverse
component v can be interpreted as the rate of motion along the
θ
circumference of a circle having a radius r. In particular, the term
ɺ
θ = dθ / dt is called the angular velocity, since it indicates the time
rate of change of the angle θ. Common units used for this
measurement are rad/s.

a b
Fig. 2-7.

Since v and v are mutually perpendicular, the magnitude of
r
θ
velocity or speed is simply the positive value of
ɺ
2
v = ()r ɺ 2 + (rθ ) 2-22
and the direction of v is, of course, tangent to the path, Fig. 2-7,b.
Acceleration. Taking the time derivatives of Eq. 2-20, using
Eqs. 2-21, we obtain the particle’s instantaneous acceleration
ɺ
ɺɺ
rθu
a = v ɺ = ru ɺɺ r + ru ɺɺ r + ɺ ɺ θ + rθu θ + rθu ɺ 2-23
θ
To evaluate u ɺ ,it is necessary only to find the change in the
θ
direction of u since its magnitude is always unity. During the time a
θ
change will not change the direction of u , however, a change will
θ
cause u to become ′ u , where ′ =u θ u θ +∆u , Fig. 2-8,a. The time
θ
θ
θ
change in u is thus ∆u . For small angles this vector has a
θ
θ
111