Page 108 - 4624

k components may be carried out in a similar manner, which yields
the final result,
dr dx dy dz
v = =i + j +k 2-11
dt dt dt dt
where

dx dy dz
v = = ; x ɺ v = = ; y ɺ v = = . z ɺ 2-12
x
dt y dt z dt
The velocity has a magnitude that is found from
2
2
v= v + v + v 2 z , 2-13
y
x
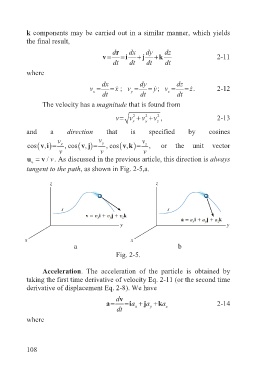
and a direction that is specified by cosines
cos ( , =v i ) v x , cos ( , =v j ) v y , cos ( , vk )= v z , or the unit vector
v v v
u v = v / v. As discussed in the previous article, this direction is always
tangent to the path, as shown in Fig. 2-5,a.

a b
Fig. 2-5.

Acceleration. The acceleration of the particle is obtained by
taking the first time derivative of velocity Eq. 2-11 (or the second time
derivative of displacement Eq. 2-8). We have

dv
a = =i a + j a +k a 2-14
dt x y z
where

108