Page 107 - 4624

40 Motion of Particle: Cartesian Coordinates

Occasionally the motion of a particle can best be described along
a path that can be expressed in terms of its x, y, z coordinates.
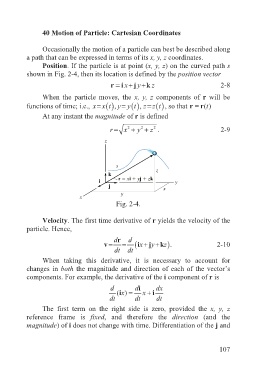
Position. If the particle is at point (x, y, z) on the curved path s
shown in Fig. 2-4, then its location is defined by the position vector
r = i x+ j y+k 2-8
z
When the particle moves, the x, y, z components of r will be
functions of time; i.e., x xt y y t= ( ), = ( ), z z t= ( ), so that r =r ()t
At any instant the magnitude of r is defined
r = x + y + z . 2-9
2
2
2

Fig. 2-4.

Velocity. The first time derivative of r yields the velocity of the
particle. Hence,
dr d
v = = ( x+ j y+k z ). 2-10
i
dt dt
When taking this derivative, it is necessary to account for
changes in both the magnitude and direction of each of the vector’s
components. For example, the derivative of the i component of r is
d ()x = di x + i dx
i
dt dt dt
The first term on the right side is zero, provided the x, y, z
reference frame is fixed, and therefore the direction (and the
magnitude) of i does not change with time. Differentiation of the j and

107