Page 48 - 4621

1
W роз ( j )
1 W ( j )
1.0 роз 1 1  W роз ( j )
K
1 2

1  K 1  K

1
1

ω p
2
ω ω p
ω

а б

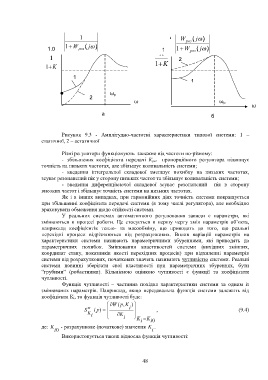
Рисунок 9.3 - Амплітудно-частотні характеристики типової системи: 1 –
статичної, 2 – астатичної

Різні регулятори функціонують залежно від частоти по-різному:
- збільшення коефіцієнта передачі К рег пропорційного регулятора підвищує
точність на низьких частотах, але збільшує коливальність системи;
- введення інтегральної складової зменшує похибку на низьких частотах,
зсуває резонансний пік у сторону низьких частот та збільшує коливальність системи;
- введення диференціюючої складової зсуває резонансний пік в сторону
високих частот і збільшує точність системи на низьких частотах.
Як і в інших випадках, при гармонійних діях точність системи покращується
при збільшенні коефіцієнта передачі системи (в тому числі регулятора), але необхідно
враховувати обмеження щодо стійкості системи.
У реальних системах автоматичного регулювання завжди є параметри, які
змінюються в процесі роботи. Це стосується в першу чергу змін параметрів об’єкта,
наприклад коефіцієнтів тепло- та масообміну, що приводить до того, що реальні
перехідні процеси відрізняються від розрахункових. Вплив варіацій параметрів на
характеристики системи називають параметричними збуреннями, які приводять до
параметричних похибок. Змінювання властивостей системи (вихідних змінних,
координат стану, показників якості перехідних процесів) при відхиленні параметрів
системи від розрахункових, початкових значень називають чутливістю системи. Реальні
системи повинні зберігати свої властивості при параметричних збуреннях, бути
“грубими” (робастними). Кільнісною оцінкою чутливості є функції та коефіцієнти
чутливості.
Функція чутливості – частинна похідна характеристики системи за одним із
змінюваних параметрів. Наприклад, якщо передавальна функція системи залежить від
коефіцієнта К і, то функція чутливості буде:
  W (p ,K ) 
S W ( ) p   i  , (9.4)
K i   K 
 i  K  K
i 0 i
де: K - розрахункове (початкове) значення K .
0 i i
Використовується також відносна функція чутливості:

48