Page 27 - 4621

тобто амплітудно-фазова характеристика ланки збігається з додатною уявною піввіссю
(рис. 4.5).
Згідно з (4.9), амплітудна і фазова частотні характеристики диференціювальної
ланки:
T   
A    T  і    arctg     . (4.10)


 0  2
Логарифмічна амплітудна характеристика ланки:
L    lg   T lg T lg  . (4.11)

Im

K  i

0   0 Re

Рисунок 4.5 - Амплітудно-фазова характеристика диференціювальної ланки

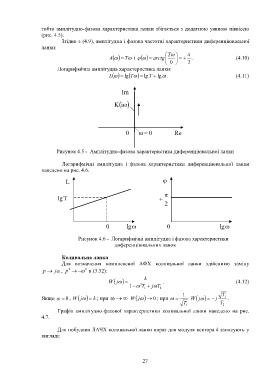
Логарифмічні амплітудна і фазова характеристики диференціювальної ланки
наведено на рис. 4.6.

L 

lg T 
 2

0 lg  0 lg 

Рисунок 4.6 - Логарифмічні амплітудна і фазова характеристики
диференціювальних ланок

Коливальна ланка
Для визначення комплексної АФХ коливальної ланки здійснимо заміну
2
p   j , p 2    в (3.32):
k
W  j  . (4.12)
1  2 T  j T
1 2
1 T
j
W
Якщо   0 ,   kjW   ; при     jW 0 ; при      j 1 .
T T
1 2
Графік амплітудно-фазової характеристики коливальної ланки наведено на рис.
4.7.

Для побудови ЛАЧХ коливальної ланки вираз для модуля вектора k записують у
вигляді:

27