Page 173 - 4617

Приклад 8. ВИМУШЕНІ КОЛИВАННЯ З УРАХУВАННЯМ ОПОРУ


59,4 30 

10t   100t
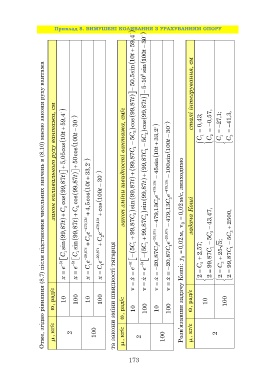
Отже, згідно рівняння (8.7) після підстановки чисельних значень в (8.10) маємо закони руху вантажа
50,5sin 3 sin 10

 5 сталі інтегрування, см

закон коливального руху вантажа, см

99,87t
 99,87t 0,57,
59,4  30 cos   0,43; 27,1; 41,3,

  2 cos 30       
10t  100t 5C 5C  2 33,2 C  1  C 2  C  1  C 2 

5,05cos 50cos   99,87C 1 99,87C 1 10t   100t 

  33,2  закон зміни швидкості вантажа, см/с      45sin 100sin
99,87t 99,87t 10t 30 99,87t    99,87t 479,13t 479,13t м/с, знаходимо

cos cos 4,5cos   100t   

2 2 cos sin sin
C C 479,13C 479,13C 0,02
    2 2 задача Коші 43,47, 2500,
  479,13t 479,13t 2 e  2 e   0
99,87t 99,87t   99,87C 99,87C 20,87t 20,87t 0,02м, v 5C  2 5C  2

sin sin C 2 e  C 2 e   5C 1  5C 1  1  1 2,57; 1 3; 1

1 1 20,87t 20,87t   25 
C C
    y 0  99,87C  99,87C
5t 5t 1 1 5t 5t 2 2
e  e  e  e  C C
    
x x x Ce  x Ce  x x x 20,87Ce  x 20,87Ce  2   2    2   2   
 v v   v 
, рад/с 10  100  10 100 та закони зміни швидкості тягарця , рад/с  10 100  10   100 Розв’язавши задачу Коші: , рад/с 10 100
v




, кг/с 2 100 , кг/с , кг/с 2

 2   100 
  

173