Page 84 - 4523

Для другої –
Y  z W  z
 zW e   1 . (2.35)
X  z 1 W 1    zWz 2

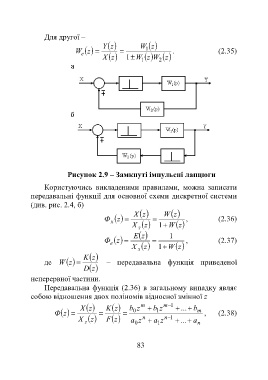
Рисунок 2.9 – Замкнуті імпульсні ланцюги
Користуючись викладеними правилами, можна записати
передавальні функції для основної схеми дискретної системи
(див. рис. 2.4, б)
X  z W  z
Ф x  z   , (2.36)
X з   z 1  W   z

Е  z 1
Ф е  z   , (2.37)
X з   z 1  W   z
K  z
де W  z  – передавальна функція приведеної
D  z
неперервної частини.
Передавальна функція (2.36) в загальному випадку являє
собою відношення двох поліномів відносної змінної z
m
X  z K  z b z  b z m1  ... b
 zФ    0 1 m , (2.38)
n
X з  z F  z a 0 z  a 1 z n1  ... a n

83