Page 11 - 4402

Потрібно:
1) побудувати емпіричну ламану регресії Y на X ;
2) вибрати вид рівняння регресії;
3) оцінити залежність між Y і X емпіричним
коефіцієнтом кореляції;
4) скласти емпіричне рівнянні регресії;
5) накреслити графік лінії регресії (у системі
координат,
використовуваної для побудови емпіричної ламаної).
Розвязок. 1) Для побудови емпіричної ламаної регресії
Y на X обчислимо середнє значення об’єму досліджуваного
газу при кожному значенні температури:
y (X  x )  3 (  5  4 ) 3  /( ) 8  . 3 37 ;
1 1
y (X  x )  4 (  10  5 ) 7  /( 17 )  . 4 41 ;
2 2
y 3 (X  x 3 )  4 (  11 5 19  6 ) 6  /( 36 )  . 4 89 ;
y (X  x )  5 (  15  6 ) 4  /( 19 )  . 5 20 ;
4 4
y (X  x )  6 (  9  7 ) 7  /( 16 )  . 6 43 ;
5 5
y (X  x )  7 ( 4 / ) 4   0 . 7
 6 6
(x , y (X  x ))
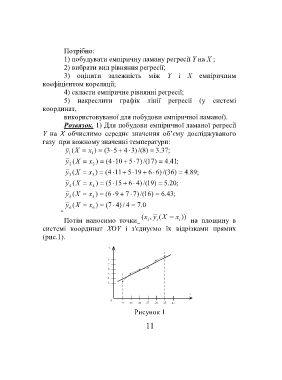
Потім наносимо точки  i i i на площину в
системі координат XОY і з'єднуємо їх відрізками прямих
(рис.1).

Рисунок 1

11