Page 9 - 4402

Теоретичні відомості

Статистичне дослідження залежностей

При дослідженні систем випадкових величин варто
розглянути питання про їх взаємозалежність або незалежність.
Зокрема, залежність однієї випадкової величини від значень
іншої називають кореляційною.
Якщо випадкові величини X і Y лише стохастично
залежні, то виникає завдання наближеного подання Y ≈f (X)
однієї величини через іншу. Самим зручним і
загальноприйнятним є наближення по методу найменших
квадратів.
Величина f (X) називається найкращим (у сенсі методу
найменших квадратів) наближенням для Y , якщо 
M ( f (X ) Y ) 2
набуває найменш можливе значення. У цьому
випадку величина f (X) − середня квадратична регресія Y на X .
Якщо параметри регресії визначають за результатами
спостережень, регресію називають емпіричною, або
вибіркової. Дані спостережень у випадку системи двох
випадкових величин X і Y записують у вигляді кореляційної
таблиці:
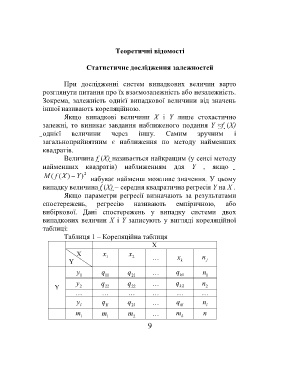
Таблиця 1 – Кореляційна таблиця
Х
Х x 1 x 2 x n
Y … k j

y 1 q 11 q 21 … q 1 k n 1
y q q … q n
Y 2 22 22 k 2 2
… … … … … …
y q q … q n
l l 1 l 2 kl l
m m m … m n
i 1 2 k
9