Page 78 - 4371


A B  A B   A B  0, а це означає, що і
1 n 2 1 n n  1

A B  A B   A B  0 , що й треба було довести.
1 1 2 2 n n

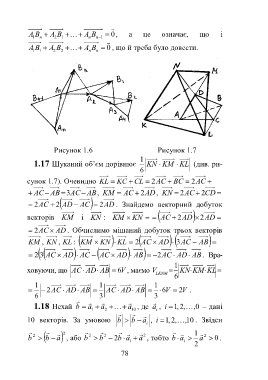
Рисунок 1.6 Рисунок 1.7
1
1.17 Шуканий об’єм дорівнює KN  KM  KL (див. ри-
6
сунок 1.7). Очевидно KL  KC  CL  AC2  BC  AC2 
 AC AB3 AC AB, KM  AC 2 AD, KN  AC2  CD2 
 2 AC 2 AD  AC  2 AD . Знайдемо векторний добуток

векторів KM і KN : KM  KN   AC  AD2  AD2 
 2 AC  AD . Обчислимо мішаний добуток трьох векторів

KM , KN , KL : KM  KN  KL  2 AC  AD   AC3  AB 
 32   AC  AD  AC  AC  AD    AB 2 AC  AD AB. Вра-
1
ховуючи, що AC AD AB  6 V , маємо V  KN KM KL 
LKNM
6
1 1 1
  2 AC  AD AB  AC  AD AB  6  V  2 V .
6 3 3
    
1.18 Нехай b  a  a   a , де a , i , 2 , 1  0 , – дані
1 2 10 i
  
10 векторів. За умовою b  b  a , i , 2 , 1  , 10 . Звідси
i
   2        1 
2
2
2
2
b  b   a , або b  b  2b  a  a , тобто ab i  a 2  0.
i
2
78