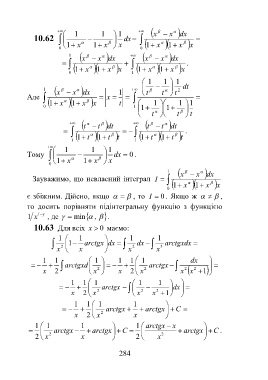Page 284 - 4371

  1 1  1  x   x  dx

10.62      dx     
0  1 x 1  x  x 0  1 x  1 x x
1 x   x  dx  x   x  dx
        .
0  1 x  1 x x 1  1 x  1 x x
 1 1  1
1 x   x  dx 1      t   2 dt
Але     x     t  t 
 1
0  1 x  1 x x t 1  1     1 1 1

 t    t   t
 t   t  dt  t   t  dt
         .
1  1 t  1 t t 1  1 t  1 t t
  1 1  1

Тому      dx  0 .
0 1   x 1 x  x
1  
x  x dx
Зауважимо, що невласний інтеграл I    
0  1 x  1 x x
є збіжним. Дійсно, якщо    , то I 0 . Якщо ж    ,
то досить порівняти підінтегральну функцію з функцією
1 x 1   , де   min  ,  .
10.63 Для всіх x  маємо:
0
1  1  1 1
 2   arctgx1 dx   2 dx   3 arctgxdx 
x  x  x x
1 1  1  1 1  1 dx 
    arctgxd       arctgx    


x 2  x 2  x 2 x 2 x 2 x 2 1  

1 1  1  1 1  
    arctgx     dx   

x 2  x 2  x 2 x 2 1  
1 1  1 1 
    arctgx   arctgx   C 
x 2  x 2 x 
1  1 1  1  arctgx  x 
  arctgx   arctgx  C    arctgx  C .


2  x 2 x  2  x 2 
284