Page 13 - 381_

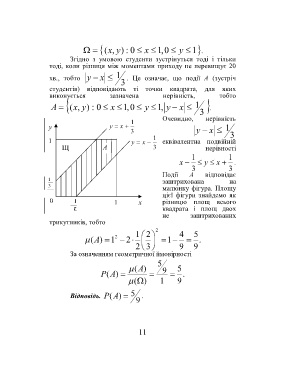
   ,( yx 0 : )  x  0 , 1  y  1 .

Згідно з умовою студенти зустрінуться тоді і тільки
тоді, коли різниця між моментами приходу не перевищує 20
хв., тобто y  x  1 . Це означає, що події А (зустріч
3
студентів) відповідають ті точки квадрата, для яких
виконується зазначена нерівність, тобто

A   ,(x : ) y 0  x  0 , 1  y  , 1 y  x  1 .
3
Очевидно, нерівність
1
у y  x  1
3 y  x 
1 3
1 y  x  еквівалентна подвійній
Щ А 3 нерівності
1 1
x   y  x  .
3 3
Події А відповідає
1
заштрихована на
3
малюнку фігура. Площу
цієї фігури знайдемо як
0 1 х різницю площ всього
квадрата і площ двох
не заштрихованих
трикутників, тобто
2
1  2  4 5
2
 (A )  1  2    1  .
2  3  9 9
За означенням геометричної ймовірності
5
(  ) A 9 5
P (A )    .
 ( ) 1 9

Відповідь. (AP )  5 .
9

11