Page 166 - 157

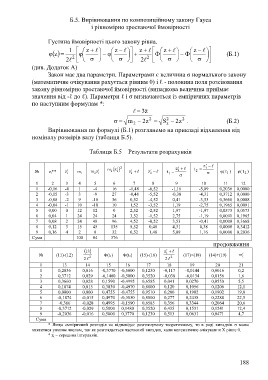
Б.5. Вирівнювання по композиційному закону Гауса
і рівномірно зростаючої ймовірності

Густина ймовірності цього закону рівна.
1    z   z    z      z   z   
  z            Ф    Ф   (Б.1)

 2 2          2 2        
(див. Додаток А)
Закон має два параметри. Параметрами є величина σ нормального закону
(математичне очікування рахується рівним 0) і ℓ - половина поля розсіювання
закону рівномірно зростаючої ймовірності (випадкова величина приймає
значення від -ℓ до ℓ). Параметри ℓ і σ визначаються із емпіричних параметрів
по наступним формулам *:
  z 3
2 2 2
  m  z 2  S  z 2 . (Б.2)
2 z
Вирівнювання по формулі (Б.1) розглянемо на прикладі відхилення від
номіналу розмірів валу (таблиця Б.5).

Таблиця Б.5 – Результати розрахунків

 z i  
2
m  z  z i   t 2 
№ z i** z m i m i z i i  z i    z i   t 1   φ( t ) φ( t )
i
1
2
i


1 2 3 4 5 6 7 8 9 10 11 12
1 -0,16 -4 1 -4 16 -1,48 -6,52 -1,16 -5,09 0,2036 0,0000
2 -0,15 -3 3 -9 27 -0,48 -5,52 -0,38 -4,31 0,3712 0,0000
3 -0,08 -2 9 -18 36 0,52 -4,52 0,41 -3,53 0,3668 0,0008
4 -0,04 -1 10 -10 10 1,52 -3,52 1,19 -2,75 0,1965 0,0091
5 0,00 0 12 12 0 2,52 -2,52 1,97 -1,97 0,0573 0,0573
6 0,04 1 24 24 24 3,52 -1,52 2,75 -1,19 0,0091 0,1965
7 0,08 2 24 48 96 4,52 -0,52 3,53 -0,41 0,0008 0,3668
8 0,12 3 15 45 135 5,52 0,48 4,31 0,38 0,0000 0,3412
9 0,16 4 2 8 32 6,52 1,48 5,09 1,16 0,0000 0,2036
Сума 100 84 376
продовження

 13 z  
i
№ (11)-(12) Ф(t 1) Ф(t 2) (15)-(16) (17)×(18) (14)+(19) m
i
2 2 2 2
1 13 14 15 16 17 18 19 20 21
1 0,2036 0,016 -0,3770 -0,5000 0,1230 -0,117 -0,0144 0,0016 0,2
2 0,3712 0,029 -0,1480 -0,5000 0,3520 -0,038 -0,0134 0,0156 1,6
3 0,3660 0,028 0,1590 -0,4995 0,6585 0,041 0,0270 0,0550 5,5
4 0,1874 0,015 0,3830 -0,4970 0,8800 0,120 0,1056 0,1206 12,1
5 0,0000 0,000 0,4755 -0,4755 0,9510 0,200 0,1902 0,1902 19,0
6 -0,1874 -0,015 0,4970 -0,3830 0,8800 0,277 0,2438 0,2288 22,5
7 -0,366 -0,028 0,4995 -0,1590 0,6585 0,356 0,3344 0,2064 20,6
8 -0,3712 -0,029 0,5000 0,1480 0,3520 0,435 0,1531 0,1241 12,4
9 -0,2036 -0,016 0,5000 0,3770 0,1230 0,513 0,0631 0,0471 4,7
Сума
* Якщо емпіричний розподіл не відповідає розглянутому теоретичному, то в ряді випадків σ може
виявитися уявним числом, так як розглядається частковий випадок, коли математичне очікування Х рівне 0.
* z i – середина інтервалів.

188