Page 171 - 157

 m n 50
1) вираховуємо m  i i   5 . 0 ;
N 100
2) для даного значення m  5 . 0 (m позначена через свій теоретичний
параметр а) знаходимо Р(m i) і проставляємо в колонці 5;
3) перемноживши Р(m i) на N=100, отримаємо вирівнювання частоти n
i
(колонка 6).
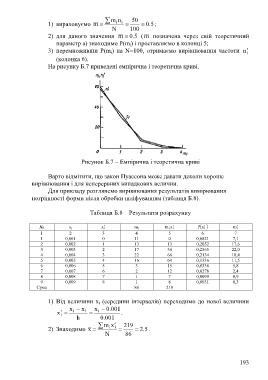
На рисунку Б.7 приведені емпірична і теоретична криві.

Рисунок Б.7 – Емпірична і теоретична криві

Варто відмітити, що закон Пуассона може давати деколи хороше
вирівнювання і для неперервних випадкових величин.
Для прикладу розглянемо вирівнювання результатів вимірювання
погрішності форми після обробки шліфуванням (таблиця Б.8).

Таблиця Б.8 – Результати розрахунку

№ х i x i m i m i x P  x m
i
i
i
1 2 3 4 5 6 7
1 0,001 0 11 0 0,0821 7,1
2 0,002 1 13 13 0,2052 17,6
3 0,003 2 17 34 0,2565 22,0
4 0,004 3 22 66 0,2134 18,4
5 0,005 4 16 64 0,1336 11,5
6 0,006 5 3 15 0,0338 5,8
7 0,007 6 2 12 0,0278 2,4
8 0,008 7 1 7 0,0099 0,9
9 0,009 8 1 8 0,0031 0,3
Сума 86 219

1) Від величини х і (середини інтервалів) переходимо до нової величини
x  x x  . 0 001

x  i 1  i .
i
h . 0 001
 m x 219
2) Знаходимо x  i i   5 . 2 .
N 86

193