Page 61 - Лекція 6

x
Знайдемо площу S під кривою y 1 , x a 0
(Рис5.1). Площу заштрихованої фігури безпосередньо
обчислити важко. Однак , якщо відрізати нескінченний “
хвіст” прямою x=b , то площу криволінійної трапеції aABb
b dx
можна обчислити за допомогою визначеного інтег-рала .
a x
Якщо b , то ми повинні отримати площу всієї
заштрихованої фігури, тобто
b dx b
S lim lim ln x b lim ln .
b x b a b a
a
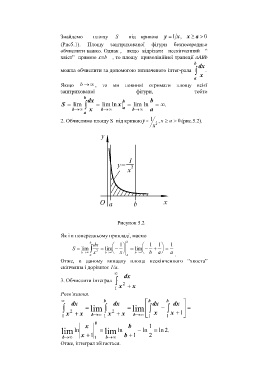
2. Обчислимо площу S під кривоюy 1 , x a 0 (рис.5.2).
x 2

Рисунок 5.2

Як і в попередньому прикладі, маємо

b dx 1 b 1 1 1
S lim 2 lim lim
b a x b x a b b a a .
Отже, в даному випадку площа нескінченного “хвоста”
скінченна і дорівнює 1/а.

dx
3. Обчислити інтеграл
x 2 x
1
Розв’язання.

dx b dx b dx b dx

x 2 x lim x 2 x lim x x 1
1 b 1 b 1 1

x b b 1
lim ln lim ln ln ln 2.

b x 1 1 b b 1 2
Отже, інтеграл збігається.