Page 65 - Лекція 6

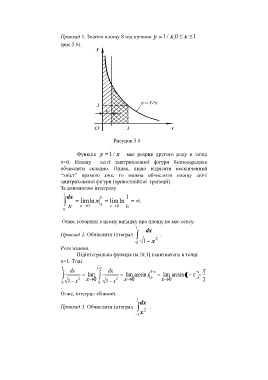
Приклад 1. Знайти площу S під кривою y 1/ x 0, x 1

(рис.5.6).

Рисунок 5.6

Функція y 1 / x має розрив другого роду в точці
x=0. Площу всієї заштрихованої фігури безпосередньо
обчислити складно. Однак, якщо відрізати нескінченний
“хвіст” прямою x= , то можна обчислити площу двічі
заштрихованої фігури (криволінійної трапеції).
За допомогою інтегралу
1 dx 1
limln x 1 lim ln .
x 0 0

Отже, говорити в цьому випадку про площу не має сенсу.
1 dx
Приклад 2. Обчислити інтеграл .
0 1 x 2
Розв’язання.
Підінтегральна функція на [0;1] невизначена в точці
x=1. Тоді

1 1
dx dx 1
lim lim arcsin x 0 lim arcsin 1
0 1 x 2 0 0 1 x 2 0 0 2
.
Отже, інтеграл збіжний.
1 dx
Приклад 3. Обчислити інтеграл .
x 2
1