Page 60 - Лекція 6

5.3 Невластиві інтеграли першого роду

Вважатимемо, що відповідна функція f x інтегрована на
будь-якому скінченному інтервалі, що міститься в
нескінченному.
b
Означення. Скінченна границя lim f ( )x dx (якщо вона
b
a
існує) називається невластивим інтегралом функції f пер-шого

роду і позначається f x dx( ) , тобто
a
b
f x dx( ) lim f x dx( ) (5.4)
b
a a
Аналогічно визначаються невластиві інтеграли для інших
нескінченних інтервалів:
b b
f x dx( ) lim f x dx( ) (5.5)
a
a
c
f x dx( ) f x dx( ) f x dx( ) , (5.6)

c
де с - будь - яке число.
Якщо існує скінченна границя (5.4), то кажуть що
невластивий інтеграл збігається . Якщо границя (5.4) не існує
або нескінченна , то інтеграл (5,4) розбігається.
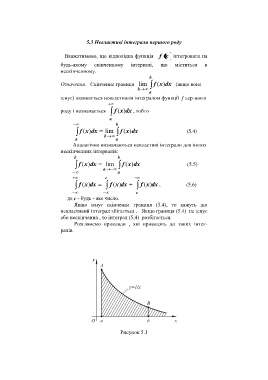
Розглянемо приклади , які приводять до таких інтег-
ралів.

Рисунок 5.1