Page 79 - 70

яка має наступний вираз:
2
z
1 
p( z ) e  2 , p( z ) p( x ) x . (3.37)
2

В додатку Г приведені значення щільності ймовірності нор-
мованої диференціальної функції нормального закону розподілу, які
можуть бути легко отримані на основі залежності (3.37).
На рис. 3.7 показаний графік нормованої диференціальної фу-
нкції ННЗР, який може бути використаний для будь-яких значень
відхилень при умові, що при z =1 x  x   . Вираз для інтеграль-
x
ної функції нормованого нормального розподілу є таким:
2
z
1 z 
Ц( z)    e 2 dz . (3.38)
2 р  

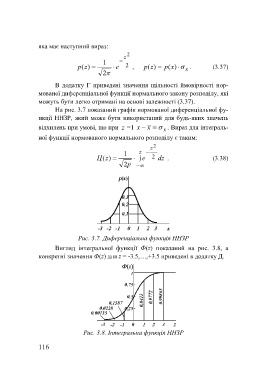
Рис. 3.7. Диференціальна функція ННЗР
Вигляд інтегральної функції Ф(z) показаний на рис. 3.8, а
конкретні значення Ф(z) для z = -3.5,…,+3.5 приведені в додатку Д.

Рис. 3.8. Інтегральна функція ННЗР

116