Page 265 - 70

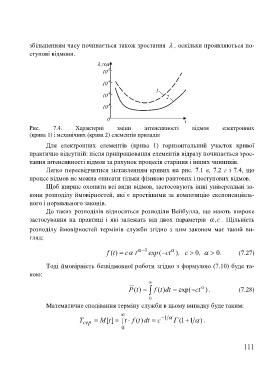
збільшенням часу починається також зростання  , оскільки проявляються по-
ступові відмови.

Рис. 7.4. Характерні зміни інтенсивності відмов електронних
(крива 1) і механічних (крива 2) елементів приладів
Для електронних елементів (крива 1) горизонтальний участок кривої
практично відсутній: після припрацювання елементів відразу починається зрос-
тання інтенсивності відмов за рахунок процесів старіння і інших чинників.
Легко пересвідчитися зіставленням кривих на рис. 7.1 в, 7.2 г і 7.4, що
процес відмов не можна описати тільки фізикою раптових і поступових відмов.
Щоб ширше охопити всі види відмов, застосовують інші універсальні за-
кони розподілу ймовірностей, які є простішими за композицію експоненціаль-
ного і нормального законів.
До таких розподілів відносяться розподіли Вейбулла, що мають широке
застосування на практиці і які залежать від двох параметрів  c , . Щільність
розподілу ймовірностей термінів служби згідно з цим законом має такий ви-
гляд:

 1  
f t ) ( c t exp ( ct , ) c  , 0   . 0 (7.27)
Тоді ймовірність безвідмовної роботи згідно з формулою (7.10) буде та-
кою:

P (t )   f (t )dt  exp( ct  ) . (7.28)
0
Математичне сподівання терміну служби в цьому випадку буде таким:

T сер  M t ] [   t  f (t )dt  c  1   (1 1  ) .
0

111