Page 22 - 6832

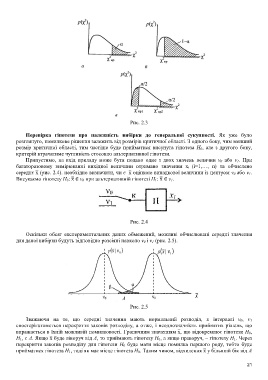
Рис. 2.3

Перевірка гіпотези про належність вибірки до генеральної сукупності. Як уже було
розглянуто, помилкове рішення залежить від розмірів критичної області. З одного боку, чим менший
розмір критичної області, тим частіше буде прийматися висунута гіпотеза H 0, але з другого боку,
критерій втрачатиме чутливість стосовно альтернативної гіпотези.
Припустимо, на вхід приладу може бути подано одне з двох значень величин v 0 або v 1. При
багаторазовому вимірюванні вихідної величини отримано значення х і (і=1,…, n) та обчислено
середнє х (рис. 2.4). необхідно визначити, чи є х оцінкою випадкової величини із центром v 0 або v 1.
Висуваємо гіпотезу H 0: х ∈ v 0 при альтернативній гіпотезі H 1: х ∈ v 1.

Рис. 2.4

Оскільки обсяг експериментальних даних обмежений, можливі обчислювані середні значення
для даної вибірки будуть відповідно розсіяні навколо v 0 і v 1 (рис. 2.5).

Рис. 2.5

Зважаючи на те, що середні значення мають нормальний розподіл, в інтервалі v 0, v 1
спостерігатиметься перекриття законів розподілу, а отже, і неоднозначність прийнятих рішень, що
виражається в їхній можливій помилковості. Граничним значенням х, що відокремлює гіпотези H 0,
H 1, є А. Якщо х буде ліворуч від А, то приймають гіпотезу H 0, а якщо праворуч, – гіпотезу H 1. Через
перекриття законів розподілу для гіпотези H 0 буде мати місце помилка першого роду, тобто буде
прийматися гіпотеза H 1, тоді як має місце гіпотеза H 0. Таким чином, відхилення х у більший бік від А

21