Page 39 - 6831

знаходять за таблицею.Якщо r s > r s*, то з ймовірністю Р > 1–α можна стверджувати, що
кореляційний зв’язок між величинами Х і Y є достовірним.
Порядок дослідження кореляційного зв’язку між ознаками Х і Y за допомогою
коефіцієнта рангової кореляції покажемо на прикладі.
Приклад. Дослідити кореляційний зв’язок між висотою і масою рослин за даними
вибірки:
Таблиця 1

Х, см 165 176 175 168 167 172 180 179 173 166
Y, кг 56 80 70 64 61 63 75 76 68 58
Рівень значущості α = 0,01.
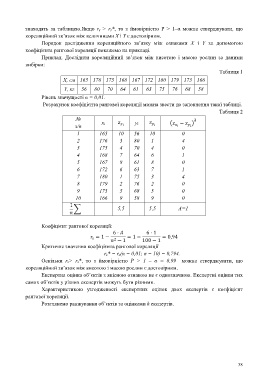
Розрахунок коефіцієнта рангової кореляції можна звести до заповнення такої таблиці.
Таблиця 2
№
х і y i −

з/п
1 165 10 56 10 0
2 176 3 80 1 4
3 175 4 70 4 0
4 168 7 64 6 1
5 167 8 61 8 0
6 172 6 63 7 1
7 180 1 75 3 4
8 179 2 76 2 0
9 173 5 68 5 0
10 166 9 58 9 0
1
5,5 5,5 A=1

Коефіцієнт рангової кореляції:
6 ⋅ 6 ⋅ 1
= 1 − = 1 − = 0,94

− 1 100 − 1
Критичне значення коефіцієнта рангової кореляції
r s* = r s(α = 0,01; n = 10) = 0,794.
Оскільки r s> r s*, то з ймовірністю Р > 1 – α = 0,99 можна стверджувати, що
кореляційний зв’язок між висотою і масою рослин є достовірним.
Експертна оцінка об’єктів з якісною ознакою не є однозначною. Експертні оцінки тих
самих об’єктів у різних експертів можуть бути різними.
Характеристикою узгодженості експертних оцінок двох експертів є коєфіцієнт
рангової кореляції.
Розглянемо ранжування об’єктів за оцінками k експертів.

38