Page 41 - 6831

∑ − ̄ = ( − 1) − , (9)

де = ∑ − 1 ..
ℓ

ℓ ℓ

∑ − ̄ − ̄ = ( − 1) − + − ∑ − . (10)

З урахуванням тотожніх співвідношень (8), (9) і (10) формула (2) для
коефіцієнта кореляції Спірмена набуває вигляду:

/ ∑

= (11)

( )/ ( )/

За умов << ( − 1), << ( − 1) формулу (11) можна спростити до

такого кінцевого вигляду:

∑

= 1 − . (12)
( )
Мірою узгодженості експертних оцінок, проведених двома експертами є коефіцієнт
рангової кореляції Спірмена.
Мірою узгодженості експертних оцінок, проведених більшою кількістю експертів
(k>2) є коефіцієнт конкордації.
Опишемо алгоритм розрахунку коефіцієнта конкордації.
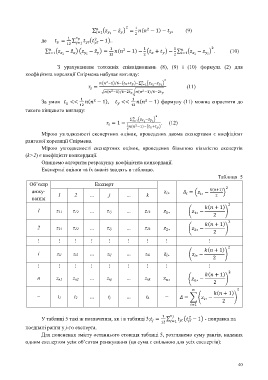
Експертні оцінки та їх аналіз зводять в таблицю.
Таблиця 5
Об’єктр Експерт

анжу- = − ( )
∗
1 2 … j … k ∗
вання

( + 1)
1 z 11 z 12 … z 1j … z 1k −
∗
∗
2
( + 1)
2 z 21 z 22 … z 2j … z 2k −
∗
∗
2
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮

( + 1)
i z i1 z i2 … z ij … z ik −
∗
∗
2
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
( + 1)
n z n1 z n2 … z nj … z nk −
∗
∗
2

( + 1)
– t 1 t 2 … t j … t k – = −
∗
2

У таблиці 5 такі ж позначення, як і в таблиці 3; = ∑ − 1 - поправка на

ℓ
ℓ ℓ
поєднані ранги у j-го експерта.
Для пояснення змісту останнього стовпця таблиці 5, розглянемо суму рангів, наданих
одним експертом усім об’єктам ранжування (ця сума є спільною для усіх експертів):
40