Page 104 - 6374

У зв’язку з тим що період модуля косинуса дорівнює , період зміни амплітуди

2
= . (34)
а
− 1
2

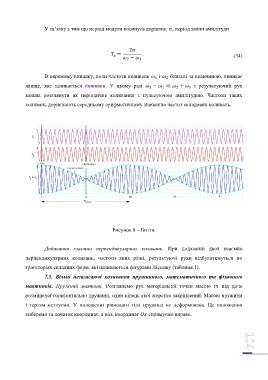
В окремому випадку, коли частоти коливань і близькі за величиною, виникає
1
2
явище, яке називається биттям. У цьому разі − ≪ + і результуючий рух
2
2
1
1
можна розглянути як періодичне коливання з пульсуючою амплітудою. Частоти таких
коливань дорівнюють середньому арифметичному значенню частот складових коливань.

Рисунок 8 – Биття.

Додавання взаємно перпендикулярних коливань. При додаванні двох взаємно

перпендикулярних коливань, частоти яких різні, результуючі рухи відбуватимуться по
траєкторіях складних форм, які називаються фігурами Ліссажу (таблиця 1).

7.5. Вільні незагасаючі коливання пружинного, математичного та фізичного
маятників. Пружний маятник. Розглянемо рух матеріальної точки масою під дією

розміщеної горизонтально пружини, один кінець якої жорстко закріплений. Масою пружини

і тертям нехтуємо. У положенні рівноваги тіла пружина не деформована. Це положення
виберемо за початок координат, а вісь координат спрямуємо вправо.