Page 116 - 6285

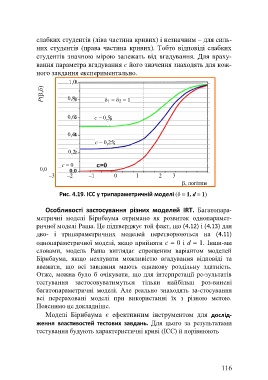
слабких студентів (ліва частина кривих) і незначним – для силь-
них студентів (права частина кривих). Тобто відповіді слабких
студентів значною мірою залежать від вгадування. Для враху-
вання параметра вгадування с його значення знаходять для кож-
ного завдання експериментально.

1,0
P(,) 0,8  1 =  2 = 1

0,6 c = 0,5

0,4
c = 0,25
0,2

c = 0
0,0

–3 –2 –1 0 1 2 3
, логіти

Рис. 4.19. ICC у трипараметричній моделі   1, d  1

Особливості застосування різних моделей IRT. Багатопара-
метричні моделі Бірнбаума отримано як розвиток однопарамет-
ричної моделі Раша. Це підтверджує той факт, що (4.12) і (4.13) для
дво- і трипараметричних моделей перетворюються на (4.11)
однопараметричної моделі, якщо прийняти c  0 і d  1. Інши-ми
словами, модель Раша виглядає спрощеним варіантом моделей
Бірнбаума, якщо нехтувати можливістю вгадування відповіді та
вважати, що всі завдання мають однакову роздільну здатність.
Отже, можна було б очікувати, що для інтерпретації ре-зультатів
тестування застосовуватимуться тільки найбільш роз-винені
багатопараметричні моделі. Але реально знаходять за-стосування
всі перераховані моделі при використанні їх з різною метою.
Пояснимо це докладніше.

Моделі Бірнбаума є ефективним інструментом для дослід-
ження властивостей тестових завдань. Для цього за результатами
тестування будують характеристичні криві (ICC) й порівнюють

116