Page 133 - 6251

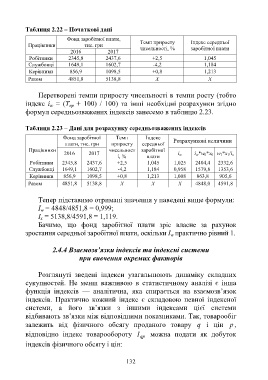
Таблиця 2.22 – Початкові дані
Фонд заробітної плати,
Темп приросту Індекс середньої
Працівники тис. грн
чисельності, % заробітної плати
2016 2017
Робітники 2345,8 2437,6 +2,5 1,045
Службовці 1649,1 1602,7 -4,2 1,184
Керівники 856,9 1098,5 +0,8 1,213
Разом 4851,8 5138,8 Х Х

Перетворені темпи приросту чисельності в темпи росту (тобто
індекс і = (Т + 100) / 100) та інші необхідні розрахунки згідно
пр
w
формул середньозважених індексів занесемо в таблицю 2.23.

Таблиця 2.23 – Дані для розрахунку середньозважених індексів

Фонд заробітної Темп Індекс
плати, тис. грн приросту середньої Розрахункові величини
Працівники чисельност заробітної
2016 2017 і w і w*w 0*x 0 w 1*x 1/і x
і, % плати
Робітники 2345,8 2437,6 +2,5 1,045 1,025 2404,4 2332,6
Службовці 1649,1 1602,7 -4,2 1,184 0,958 1579,8 1353,6
Керівники 856,9 1098,5 +0,8 1,213 1,008 863,8 905,6
Разом 4851,8 5138,8 Х Х Х 4848,0 4591,8

Тепер підставимо отримані значення у наведені вище формули:
І = 4848/4851,8 = 0,999;
w
І = 5138,8/4591,8 = 1,119.
x
Бачимо, що фонд заробітної плати зріс власне за рахунок
зростання середньої заробітної плати, оскільки І практично рівний 1.
w

2.4.4 Взаємозв’язки індексів та індексні системи

при вивчення окремих факторів

Розглянуті зведені індекси узагальнюють динаміку складних

сукупностей. Не менш важливою в статистичному аналізі є інша
функція індексів — аналітична, яка спирається на взаємозв’язок
індексів. Практично кожний індекс є складовою певної індексної
системи, а його зв’язки з іншими індексами цієї системи

відбивають зв’язки між відповідними показниками. Так, товарообіг
залежить від фізичного обсягу проданого товару q і цін p,

відповідно індекс товарообороту I можна подати як добуток
qp
індексів фізичного обсягу і цін:

132