Page 36 - 4700

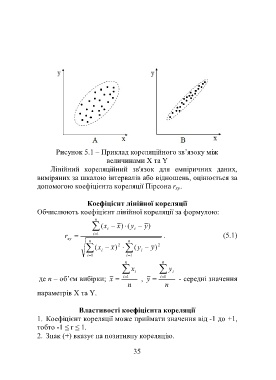
Рисунок 5.1 – Приклад кореляційного зв’язоку між
величинами X та Y
Лінійний кореляційний зв'язок для емпіричних даних,
виміряних за шкалою інтервалів або відношень, оцінюється за
допомогою коефіцієнта кореляції Пірсона r xy.

Коефіцієнт лінійної кореляції
Обчислюють коефіцієнт лінійної кореляції за формулою:
n
 x ( i  x)  y( i  y)
r   i 1 . (5.1)
xy
n n
 x ( i  x) 2   y ( i  y) 2
 i 1  i 1
n n
 x i  y i
де n – об’єм вибірки; x  i1 , y  i1 - середні значення
n n
параметрів X та Y.

Властивості коефіцієнта кореляції
1. Коефіцієнт кореляції може приймати значення від -1 до +1,
тобто -1 ≤ r ≤ 1.
2. Знак (+) вказує на позитивну кореляцію.

35