Page 216 - 4685
P. 216
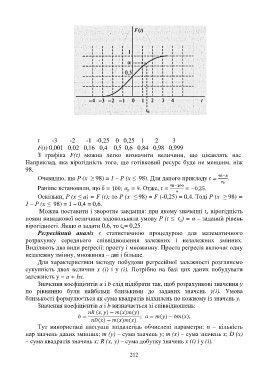
t -3 -2 -1 -0,25 0 0,25 1 2 3
F(t) 0,001 0,02 0,16 0,4 0,5 0,6 0,84 0,98 0,999
З графіка F(t) можна легко визначити величини, що цікавлять нас.
Наприклад, яка вірогідність того, що готівковий ресурс буде не меншим, ніж
98.
)
Очевидно, що Р (х ≥ 98) = 1 – Р (х ≤ 98). Для даного прикладу ' = .
Раніше встановили, що 0 = 100; = 9. Отже, ' = !ll = −0,25.
)
Оскільки, Р (х ≤ а) = F (t); то Р (х ≤ 98) = F (-0,25) = 0,4. Тоді Р (х ≥ 98) =
1 – Р (х ≤ 98) = 1 – 0,4 = 0,6.
Можна поставити і зворотне завдання: при якому значенні t вірогідність
а
появи випадкової величини задовольняла умову Р (t ≤ t ) = α – заданий рівень
a
вірогідності. Якщо α задати 0,6, то t = 0,25.
α
Регресійний аналіз є статистичною процедурою для математичного
розрахунку середнього співвідношення залежних і незалежних змінних.
Виділяють два види регресії: просту і множинну. Проста регресія включає одну
незалежну змінну, множинна – дві і більше.
Для характеристики методу побудови регресійної залежності розглянемо
сукупність двох величин х (i) і у (i). Потрібно на базі цих даних побудувати
залежність у = а + bх.
Значення коефіцієнтів а і b слід підібрати так, щоб розрахункові значення у
по рівнянню були найбільш близькими до заданих значень у(i). Умова
близькості формулюється як сума квадратів відхилень по кожному із значень у.
Значення коефіцієнтів а і b визначається зі співвідношень:
I 4, ( − E4E(
0 = ; 1 = E( − 0E4.
IG4 − E4E4
Тут використані наступні заздалегідь обчислені параметри: п – кількість
пар значень даних змінних; т (у) – сума значень y; т (х) – сума значень х; D (х)
– сума квадратів значень х; R (х, y) – сума добутку значень х (i) і y (i).
212