Page 215 - 4685

Коефіцієнт варіабельності:
ƒ ) 9
† = = = 0,09
)
0 100
Якнайповнішою характеристикою випадкової величини є закон її
розподілу. Він показує, яка вірогідність появи кожного можливого значення
випадкової величини або яким чином сумарна вірогідність появи випадкової
величини, що дорівнює одиниці, розподілена між її можливими значеннями.
Іншими словами, закон розподілу встановлює зв'язок між можливими
значеннями випадкової величини і вірогідністю їх появи.
Із безлічі законів найбільш поширений нормальний закон розподілу, за
допомогою якого вирішують різні завдання оптимізації, у тому числі і в умовах
невизначеності.
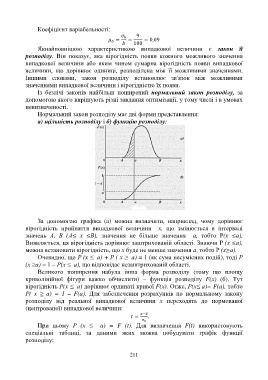
Нормальний закон розподілу має дві форми представлення:
а) щільність розподілу і б) функцію розподілу:

За допомогою графіка (а) можна визначити, наприклад, чому дорівнює

вірогідність прийняття випадкової величини х, що змінюється в інтервалі
значень А, В (А≤ х ≤В), значення не більше значення а, тобто Р(х ≤а).
Виявляється, ця вірогідність дорівнює заштрихованій області. Знаючи Р (х ≤а),
можна встановити вірогідність, що х буде не менше значення а, тобто Р (х≥а).
Очевидно, що Р (х ≤ а) + Р ( х ≥ а) = 1 (як сума несумісних подій), тоді Р
(х ≥а) = 1 – Р(х ≤ а), що відповідає незаштрихованій області.
Великого поширення набула інша форма розподілу (тому що площу
криволінійної фігури важко обчислити) – функція розподілу F(x) (б). Тут
вірогідність Р(х ≤ а) дорівнює ординаті кривої F(x). Отже, Р(х≤ а)= F(a), тобто
Р( х ≥ а) = 1 – F(a). Для забезпечення розрахунків по нормальному закону
розподілу від реальної випадкової величини х переходять до нормованої
(центрованої) випадкової величини:
XX̅
' = .
‡ ˆ
При цьому Р (х ≤ а) = F (t). Для визначення F(t) використовують
спеціальні таблиці, за даними яких можна побудувати графік функції
розподілу:

211