Page 33 - 4621

6. СТІЙКІСТЬ САК

У лекції описано суть стійкості САК, види та умови стійкості, залежність
стійкості від виду рівняння, яке описує динаміку САК.
Стійкість автоматичної системи  це властивість системи повертатись в
початковий стан рівноваги після припинення дій збурення, яке вивело систему з
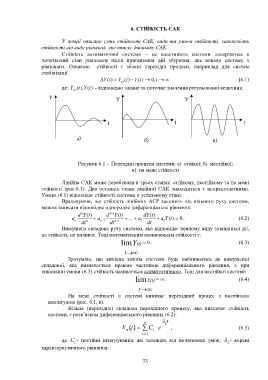
рівноваги. Ознакою стійкості є збіжні перехідні процеси, наприклад для систем
стабілізації
Y( t)  Y ( t) Y( t)  ,0 t   (6.1)
зд
де: Y (t ),Y ) (t - відповідно задане та поточне значення регульованої величини.
зд

Y Y Y

t t t

а) б) в)

Рисунок 6.1 - Перехідні процеси системи: а) стійкої; б) нестійкої;
в) на межі стійкості

Лінійна САК може перебувати в трьох станах: стійкому, нестійкому та на межі
стійкості (рис.6.1). Два останніх стани лінійної САК знаходиться є непрацездатними.
Умова (6.1) відповідає стійкості системи в усталеному стані.
Враховуючи, що стійкість лінійних АСР залежить від вільного руху системи,
можна записати відповідне однородне диференціальне рівняння:
d n Y (t ) d n 1  Y (t ) dY (t )
a  a   a  Ya t ) (  0 . (6.2)
n n n 1  n 1  1 0
dt dt dt
Вимушена складова руху системи, яка відповідає певному виду зовнішньої дії,
на стійкість не впливає. Тоді математичним визначенням стійкості є:
lim (t)Y  0. (6.3)

t  
Зрозуміло, що вихідна змінна системи буде наближатись до вимушеної
складової, яка визначається правою частиною диференціального рівняння, а при
виконанні умови (6.3) стійкість називається асимптотичною. Тоді для нестійкої системи
lim Y(t)  . (6.4)

t  
На межі стійкості в системі виникає перехідний процес з постійною
амплітудою (рис. 6.1, в).
Вільна (перехідна) складова перехідного процесу, яка визначає стійкість
системи, є розв’язком диференціального рівняння (6.2):

n  i t
X ( t)   C i  e , (6.5)
n
 i 1
де C - постійні інтегрування, які залежать від початкових умов;  - корені
i
i
характеристичного рівняння:
33