Page 72 - 4495

композиція безперервних функцій між топологічними просторами
сама безперервна). Ця операція композиції завжди задовольняє зако-
ну асоціативності;
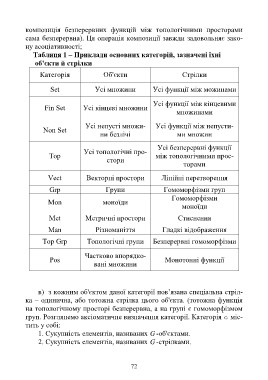
Таблиця 1 – Приклади основних категорій, зазначені їхні

об'єкти й стрілки

Категорія Об'єкти Стрілки

Set Усі множини Усі функції між можинами

Усі функції між кінцевими
Fin Set Усі кінцеві множини
множинами

Усі непусті множи- Усі функції між непусти-
Non Set
ни безлічі ми множин

Усі безперервні функції
Усі топологічні про-
Top між топологічними прос-
стори
торами

Vect Векторні простори Лінійні перетворення

Grp Групи Гомоморфізми груп
Гомоморфізми
Mon моноїди
моноїди

Met Метричні простори Стиснення

Man Різноманіття Гладкі відображення

Top Grp Топологічні групи Безперервні гомоморфізми

Частково впорядко-
Pos Монотонні функції
вані множини

в) з кожним об'єктом даної категорії пов’язана спеціальна стріл-
ка – одинична, або тотожна стрілка цього об'єкта. (тотожна функція

на топологічному просторі безперервна, а на групі є гомоморфізмом
груп. Розглянемо аксіоматичне визначення категорії. Категорія G міс-
тить у собі:

1. Сукупність елементів, називаних G -об'єктами.
2. Сукупність елементів, називаних G -стрілками.

72