Page 72 - 4371

прямокутника і напрямивши осі так, щоб сторона AB ле-
жала на осі OX , сторона AD – на осі OY (див. рисунок
1.1). Якщо сторони прямокутника рівні a і b , то коорди-
нати вершин прямокутника у цій системі координат бу-
дуть: A  0,0 , 0   ,, B a , 0 0   ,, C a , b 0 , D  ,0 b ,  0 . Нехай
M x, y,  z – довільна точка простору, тоді

MA  x  , y ,  z , MB  a  x , y,  z  , MC  a x, b y,  z  ,
MD   x , b  y ,  z . Шукані рівності легко одержуються
безпосереднім обчисленням.

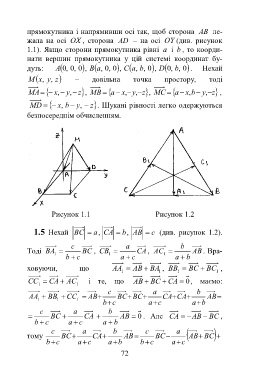
Рисунок 1.1 Рисунок 1.2

a
1.5 Нехай BC  , CA  b, AB  c (див. рисунок 1.2).
c a b
Тоді BA  BC , CB  CA , AC  AB . Вра-
1 1 1
b  c a  c a  b
ховуючи, що AA  AB  BA , BB  BC  BC ,
1 1 1 1
CC  CA  AC і те, що AB  BC  CA  0, маємо:
1 1
c a b
AA  BB  CC  AB  BC BC  CA CA  AB 
1 1 1
b c a c a b
c a b
 BC  CA  AB  0 . Але CA   AB  BC ,
b  c a  c a  b
c a b c a
тому BC  CA  AB  BC  AB  BC 
b c a c a b b c a c
72