Page 172 - 4371

2 m m 4 m m 2 m m
S  S  S     const .
ABC сегм.
a 3 a 3 a

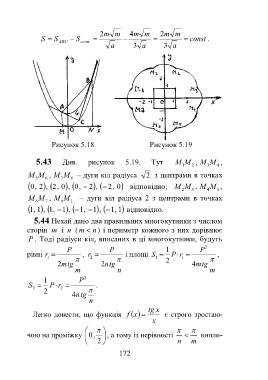
Рисунок 5.18 Рисунок 5.19

5.43 Див. рисунок 5.19. Тут M M , M M ,
1 2 3 4
M M , M M – дуги кіл радіуса 2 з центрами в точках
5 6 7 8
 ,0 2   ,2, 0   ,0,  2   2,  ,  0 відповідно; M M , M M ,
2 3 4 5

M M , M M – дуги кіл радіуса 2 з центрами в точках
6 7 8 1
   ,1,1,1  1   1,  ,  1   1,   1 , відповідно.
5.44 Нехай дано два правильних многокутники з числом
n
сторін m і n (m  ) і периметр кожного з них дорівнює
P . Тоді радіуси кіл, вписаних в ці многокутники, будуть
P P 1 P 2
рівні r  , r  і площі S  P r  ,
1  2  1 2 1 
2 m tg n 2 tg 4 m tg
m n m
1 P 2
S  P r  .
2 2
2 
4 n tg
n
tg x
Легко довести, що функція  xf  є строго зростаю-
x
    
чою на проміжку  ,0  , а тому із нерівності  випли-
 2  n m
172