Page 151 - 4371

 2 a  x  tg
2
2
xtg   або x  xtg   2 a 2 x; xtg   3 x 2 a ,
1 tg 2 
2
2
2
тоді y  x 2 tg    x 23  a x , тобто y  x 3 2  2 ax ,
2 2
 a  a
2
y  3 x    .

 3  3
2
 a 
 x  2
 3  y
Остаточно: 2  2  1 – гіпербола.
 a   a 
   


 3   3 

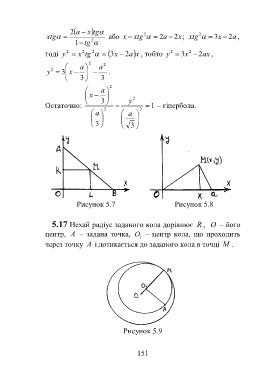
Рисунок 5.7 Рисунок 5.8

5.17 Нехай радіус заданого кола дорівнює R , O – його
центр, A – задана точка, O – центр кола, що проходить
1
через точку A і дотикається до заданого кола в точці M .

Рисунок 5.9

151