Page 54 - 4169
P. 54
Для визначення коефіцієнта Фехнера спочатку необхідно знайти середні
значення ознак. Використавши формулу середньої арифметичної простої,
отримаємо x 10 3 , млн. грн., y =11,3 млн. грн.
А отже, Кф = (8 - 2) / (8 + 2) = 0,6.
За даними табл. 6.1 розрахуємо й інші коефіцієнти рангової кореляції:
6 12 ( 2 45 ) 2
1 , 0 927 , 0 822
2
10 ( 10 ) 1 10 ( 10 ) 1
Знак коефіцієнта вказує на напрям зв’язку. А щільність можна визначити,
скориставшись шкалою для емпіричного кореляційного відношення (табл. 5.3).
Обчислені значення свідчать про прямий сильний зв'язок між вартістю
основних засобів та випуском продукції.
Отже, коефіцієнт Кендела оцінює зв'язок між ознаками обережніше, ніж
коефіцієнт Спірмена.
Перевагою коефіцієнтів рангової кореляції є простота методики
розрахунку і швидкість оцінки взаємозв’язку явищ.
Графічний метод виявлення кореляційної залежності полягає в
зображенні статистичних характеристик, добутих внаслідок зведення і
групування вихідної інформації, та наочно показує форму зв’язку між
досліджуваними ознаками та його напрям. Побудувавши графік за даними
задачі, отримаємо кореляційне поле..
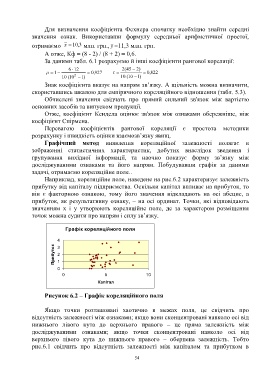
Наприклад, кореляційне поле, наведене на рис.6.2 характеризує залежність
прибутку від капіталу підприємства. Оскільки капітал впливає на прибуток, то
він є факторною ознакою, тому його значення відкладають на осі абсцис, а
прибуток, як результативну ознаку, – на осі ординат. Точки, які відповідають
значенням х і у утворюють кореляційне поле, де за характером розміщення
точок можна судити про напрям і силу зв’язку.
Графік кореляційного поля
4
3
Прибуток 2
1
0
0 5 10
Капітал
Рисунок 6.2 – Графік кореляційного поля
Якщо точки розташовані хаотично в межах поля, це свідчить про
відсутність залежності між ознаками; якщо вони сконцентровані навколо осі від
нижнього лівого кута до верхнього правого – це пряма залежність між
досліджуваними ознаками; якщо точки сконцентровані навколо осі від
верхнього лівого кута до нижнього правого – обернена залежність. Тобто
рис.6.1 свідчить про відсутність залежності між капіталом та прибутком в
54