Page 89 - 2579

для кожного рівня достовірності α з таблиць
нормального розподілу можна
 m 
  t D
  
 N 
знайти таку величину t α, при якій точність
обчислюватиметься за формулою
Якщо α = 0,05, то t a = 1,96, а якщо α = 0,003, то
t α= 3.
Підставимо у формулу (4.17) вираз дисперсії

p 1 p 
  t . Звідси

N  1
p 1 p 
2
N  t  2  1 (4.18)


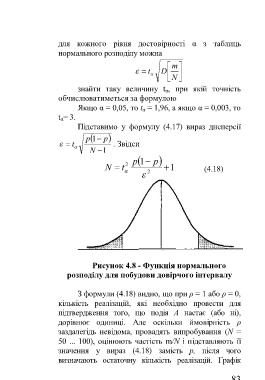
Рисунок 4.8 - Функція нормального
розподілу для побудови довірчого інтервалу

З формули (4.18) видно, що при ρ = 1 або ρ = 0,
кількість реалізацій, які необхідно провести для
підтвердження того, що подія А настає (або ні),
дорівнює одиниці. Але оскільки ймовірність ρ
заздалегідь невідома, провадять випробування (Ν =
50 ... 100), оцінюють частість m/Ν і підставляють її
значення у вираз (4.18) замість р, після чого
визначають остаточну кількість реалізацій. Графік

83