Page 90 - 2579

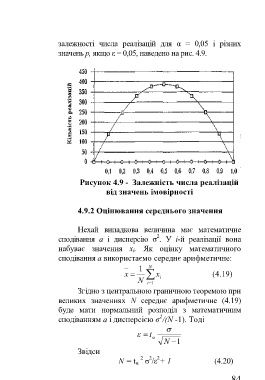
залежності числа реалізацій для α = 0,05 і різних
значень р, якщо ε = 0,05, наведено на рис. 4.9.

Рисунок 4.9 - Залежність числа реалізацій
від значень імовірності

4.9.2 Оцінювання середнього значення

Нехай випадкова величина має математичне
2
сподівання а і дисперсію σ . У і-й реалізації вона
набуває значення х i. Як оцінку математичного
сподівання а використаємо середнє арифметичне:
1 N
x  x (4.19)
i
N  i 1
Згідно з центральною граничною теоремою при
великих значеннях N середнє арифметичне (4.19)
буде мати нормальний розподіл з математичним
2
сподіванням а і дисперсією σ /(Ν -1). Тоді

  t

N  1
Звідси
2
2 2
N = t α σ /ε + 1 (4.20)
84