Page 97 - 203_

Найпростіший спосіб наближеного обчислення визначених інтегралів випливає з
означення останього. Поділимо відрізок  ba, на рівні частини точками
b  a
x  a  k , k  , 1 , 0   n , (11.1)
k
n
і покладемо
b n 1
b  a  x  x 
 f  dxx    f k n 1  . (11.2)
a n k 1  2 
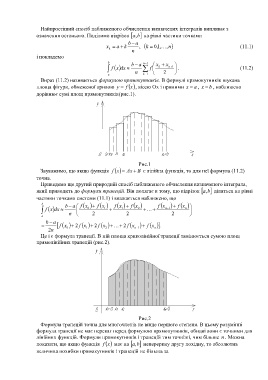
Вираз (11.2) називається формулою прямокутників. В формулі прямокутників шукана
a
b
площа фігури, обмеженої кривою y  f  x , віссю Ох і прямими x  , x  , наближено
дорівнює сумі площ прямокутників(рис.1).

Рис.1
Зауважимо, що якщо функція   Axxf   B є лінійна функція, то для неї формула (11.2)
точна.
Приведемо ще другий природній спосіб наближеного обчислення визначеного інтеграла,
який приводить до формули трапецій. Він полягає в тому, що відрізок  ba, ділиться на рівні
частини точками системи (11.1) і вважається наближено, що
b b  a  f  x  f  x f   f   f x  f  x 
x
x
 f  dxx   0 1  1 2   n 1 n 
a n  2 2 2 
b  a
x
 f   2 fx    2 fx     2 f x n 1  f  .x n
0
2
1
2n
Це і є формула трапеції. В ній площа криволінійної трапеції замінюється сумою площ
прямолінійних трапецій (рис.2).

Рис.2
Формула трапецій точна для многочленів не вище першого степеня. В цьому розумінні
формула трапеції не має переваг перед формулою прямокутників, обидві вони є точними для
лінійних функцій. Формули прямокутників і трапецій тим точніші, чим більше n . Можна
показати, що якщо функція  xf має на  ba, неперервну другу похідну, то абсолютна
величина похибки прямокутників і трапецій не більша за