Page 61 - 169

y
Вища точність

Низька точність

0 x

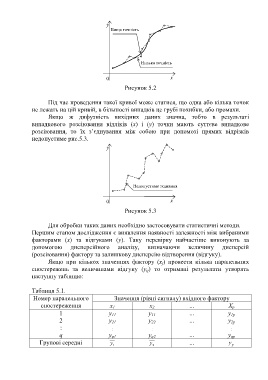
Рисунок 5.2

Під час проведення такої кривої може статися, що одна або кілька точок
не лежать на цій кривій, в більшості випадків це грубі похибки, або промахи.
Якщо ж дифузність вихідних даних значна, тобто в результаті
випадкового розсіювання відліків (x) і (y) точки мають суттєве випадкове
розсіювання, то їх з’єднування між собою при допомозі прямих відрізків
недопустиме рис.5.3.
y

Недопустиме зєднання

0 x

Рисунок 5.3

Для обробки таких даних необхідно застосовувати статистичні методи.
Першим етапом дослідження є виявлення наявності залежності між вибраними
факторами (x) та відгуками (y). Таку перевірку найчастіше виконують за
допомогою дисперсійного аналізу, визначаючи величину дисперсій
(розсіювання) фактору та залишкову дисперсію відтворення (відгуку).
Якщо при кількох значеннях фактору (x j) провести кілька паралельних
спостережень за величинами відгуку (y ij) то отримані результати утворять
наступну таблицю:

Таблиця 5.1.
Номер паралельного Значення (рівні сигналу) вхідного фактору
спостереження x 1 x 2 … X p
1 y 11 y 11 … y 1p
2 y 21 y 22 … y 2p
: : : :
q y q1 y q2 … y qp
Групові середні y y … y
1 2 p